Boolean Algebra over Trapdoor Sets: A Practical Framework for
Privacy-Preserving Set Operations with Probabilistic Guarantees

Alexander Towell Department of Computer Science
Southern Illinois University Edwardsville
Email: atowell@siue.edu

Abstract

We present Hash-Based Oblivious Sets (HBOS), a practical framework for privacy-preserving set operations that combines cryptographic hash functions with probabilistic data structures. Unlike traditional approaches using fully homomorphic encryption or secure multi-party computation, HBOS achieves microsecond-scale performance by embracing approximate operations with explicitly managed error rates.

HBOS provides oblivious representation through one-way hash transformations—the underlying data cannot be recovered from hash values. Operations return Bernoulli Booleans: plaintext approximate results with explicit error rates (false positive rate $\alpha$ , false negative rate $\beta$ ). This layered model trades full obliviousness of query results for practical efficiency, making it suitable for applications where query patterns are not sensitive or results are shared.

Our framework provides: (1) a systematic approach to propagating error bounds through composed set operations using Bernoulli type composition rules, (2) efficient Boolean and symmetric difference operations on hash-transformed data with quantifiable false positive rates, and (3) practical implementations of privacy-preserving primitives including private set intersection and secure aggregation. We build upon established techniques from probabilistic data structures (Bloom filters, HyperLogLog) while adding cryptographic privacy through one-way hash transformations.

Experimental evaluation demonstrates that HBOS operations complete in 0.4-2.1 microseconds for typical workloads, offering 1000-10000× speedup over homomorphic encryption approaches. The framework provides false positive rates bounded by hash collision probability (e.g., $2^{-256}$ for SHA-256), with privacy guarantees that depend on input entropy and threat model assumptions. We validate HBOS through implementations of private set intersection, secure deduplication, and federated learning aggregation, showing practical applicability where approximate results with explicit error bounds are acceptable.

Index Terms:

cryptographic hash functions, oblivious data structures, privacy-preserving computation, approximate algorithms, probabilistic data structures

I Introduction

The proliferation of cloud computing and data analytics has created an urgent need for privacy-preserving computational frameworks that enable operations on sensitive data without exposing the underlying values. Traditional approaches to this problem fall into two categories: cryptographic techniques such as fully homomorphic encryption (FHE) [18] and secure multi-party computation (MPC) [34], and statistical techniques such as differential privacy [12]. While powerful, these approaches often suffer from computational overhead that limits their practical deployment.

We present Hash-Based Oblivious Sets (HBOS), a practical framework that achieves efficient privacy-preserving set operations by combining cryptographic hash functions with probabilistic data structures. Our approach differs from existing solutions by explicitly embracing approximation, making error rates transparent throughout the computational pipeline. This design choice enables HBOS to achieve microsecond-scale performance while providing privacy bounded by hash collision probabilities.

The core insight underlying HBOS is that many real-world applications can tolerate controlled error rates in exchange for efficiency and privacy. By using cryptographic hash functions as one-way transformations, we map sensitive data into a hash domain where equality testing is preserved probabilistically while the original values remain computationally hidden. All subsequent operations work exclusively on these hash values, never requiring access to the plaintext. This approach builds upon well-established techniques from probabilistic data structures while adding cryptographic privacy guarantees.

HBOS embodies a layered privacy model: the hash representation is oblivious (underlying values cannot be recovered), while operations return Bernoulli Booleans—plaintext approximate results with explicit error rates. This separation is key to understanding HBOS’s guarantees: we hide what the data is, but not the pattern of query results. The framework draws on Bernoulli type theory [31], which provides systematic error propagation rules for composed approximate operations.

I-A Motivating Example

Consider a healthcare consortium where multiple hospitals need to identify patients enrolled in overlapping clinical trials without revealing their complete patient lists. Traditional approaches would require either: (1) a trusted third party to perform the intersection, violating privacy requirements, (2) homomorphic encryption with prohibitive computational costs, or (3) complex MPC protocols requiring multiple rounds of communication.

Using HBOS, each hospital can:

1.

Transform patient identifiers using a shared cryptographic hash function
2.

Perform set intersection directly on hash values
3.

Obtain results with explicit error bounds (e.g., hash collision rate $<2^{-256}$ )
4.

Complete the entire operation in milliseconds rather than minutes

This example illustrates HBOS’s key advantage: practical performance with quantifiable privacy guarantees.

I-B Contributions

This paper makes the following contributions:

•

Systematic Error Propagation: We provide a formal framework for propagating error bounds through composed set operations on hash-transformed data, enabling applications to reason about accuracy-privacy trade-offs.
•

Practical Implementation: We demonstrate that combining cryptographic hashing with probabilistic data structures achieves microsecond-scale performance for privacy-preserving set operations, offering 1000-10000× speedup over homomorphic encryption.
•

Integration of Existing Techniques: We show how established algorithms (Bloom filters, HyperLogLog) can be enhanced with cryptographic privacy guarantees through systematic application of hash transformations.
•

Real-World Applications: We validate HBOS through implementations of private set intersection, secure deduplication, and federated learning aggregation, demonstrating practical utility where approximate results are acceptable.
•

Security Analysis: We provide formal analysis showing that privacy is bounded by the collision probability of the underlying hash function, with explicit quantification of error rates.

I-C Paper Organization

The remainder of this paper is organized as follows. Section II provides background on cryptographic hash functions, Bernoulli Booleans, and threat model. Section III presents the HBOS framework design, including the layered privacy model distinguishing oblivious representation from Bernoulli query results. Section IV develops the mathematical foundations and security analysis. Section V describes our implementation and optimization techniques. Section VI evaluates performance and security properties. Section VII explores applications across multiple domains. Section VIII discusses related work. Section IX concludes.

II Background and Threat Model

II-A Cryptographic Hash Functions

A cryptographic hash function $H:\{0,1\}^{*}\rightarrow\{0,1\}^{n}$ maps arbitrary-length inputs to fixed-size outputs while satisfying three key properties:

Definition 1 (Preimage Resistance).

Given hash value $h$ , finding any $x$ such that $H(x)=h$ requires $O(2^{n})$ operations.

Definition 2 (Second Preimage Resistance).

Given $x_{1}$ , finding $x_{2}\neq x_{1}$ such that $H(x_{1})=H(x_{2})$ requires $O(2^{n})$ operations.

Definition 3 (Collision Resistance).

Finding any pair $(x_{1},x_{2})$ where $x_{1}\neq x_{2}$ and $H(x_{1})=H(x_{2})$ requires $O(2^{n/2})$ operations.

HBOS leverages these properties to create one-way transformations that preserve equality testing probabilistically while preventing recovery of original values.

II-B Approximate Data Structures

Approximate data structures trade perfect accuracy for improved space or time complexity. The canonical example is the Bloom filter [1], which supports membership queries with false positives but no false negatives. HBOS builds upon these well-established techniques, adding cryptographic privacy through hash transformations while maintaining explicit error bounds.

Definition 4 (Approximate Boolean).

An approximate Boolean value is a tuple $(v,\alpha,\beta)$ where $v\in\{\mathsf{true},\mathsf{false}\}$ is the observed value, $\alpha$ is the false positive rate (probability of observing true when latent value is false), and $\beta$ is the false negative rate (probability of observing false when latent value is true).

Definition 5 (Bernoulli Boolean).

A Bernoulli Boolean $\mathcal{B}\langle\mathbb{B}\rangle$ is an observed boolean $\tilde{b}$ with error rates $(\alpha,\beta)$ where:

•

$\alpha=\mathbb{P}[\tilde{b}=\mathsf{true}\mid b=\mathsf{false}]$ (false positive rate)
•

$\beta=\mathbb{P}[\tilde{b}=\mathsf{false}\mid b=\mathsf{true}]$ (false negative rate)

We distinguish second-order Bernoulli Booleans where $\alpha\neq\beta$ (asymmetric errors, as in Bloom filters and hash-based membership) from first-order where $\alpha=\beta$ (symmetric errors). HBOS produces second-order Bernoulli Booleans with $\alpha=2^{-n}$ (hash collision) and $\beta=0$ (no false negatives).

Definition 6 (Confusion Matrix).

The error behavior of a Bernoulli Boolean is fully characterized by its confusion matrix:

Q=\begin{pmatrix}1-\alpha&\alpha\\ \beta&1-\beta\end{pmatrix}

where $Q_{ij}=\mathbb{P}[\tilde{b}=j\mid b=i]$ gives the probability of observing $j$ given latent value $i$ . Key properties:

•

Identity matrix ( $\alpha=\beta=0$ ): perfect observation, no privacy
•

Rank-1 matrix ( $\alpha+\beta=1$ ): complete information loss, optimal privacy
•

Rank-2 matrix ( $\alpha+\beta<1$ ): information preserved, privacy/utility trade-off

For HBOS with $\alpha=2^{-n}$ and $\beta=0$ , the confusion matrix is nearly identity—high utility but query results are observable (the “concession” discussed in Section III-C).

Remark 7 (Latent vs. Observed Values).

We distinguish latent values (true mathematical objects, denoted $b, S, f$ ) from observed values (computed approximations with error rates, denoted $\tilde{b},\tilde{S},\tilde{f}$ ). This duality is fundamental: HBOS operates entirely on observed values while reasoning about their relationship to latent values through error bounds.

II-C Threat Model

We consider an honest-but-curious adversary model where:

•

Participants follow the protocol correctly but attempt to learn additional information
•

The adversary has access to hash values but cannot invert the hash function
•

The adversary may have auxiliary information about the data distribution
•

The cryptographic hash function is modeled as a random oracle

We explicitly exclude:

•

Malicious adversaries who deviate from the protocol
•

Side-channel attacks on the implementation
•

Quantum adversaries (though post-quantum hash functions could be used)

III System Design

III-A Core Abstractions

HBOS is built around three core abstractions that compose to enable complex privacy-preserving operations:

III-A1 Hash-Oblivious Values

A hash-oblivious value encapsulates the one-way transformation of sensitive data through cryptographic hashing. The key insight is that equality testing on hash values preserves the equality relation probabilistically while preventing recovery of original values. For equality testing, the false positive rate (reporting equality when values differ) equals the hash collision probability (e.g., $2^{-256}$ for SHA-256). Note that this bounds collision errors, not privacy—privacy depends on input entropy and resistance to dictionary attacks. Implementation details are provided in Appendix A.

III-A2 Approximate Values

All operations in HBOS return approximate values with explicit error rates. Each approximate value maintains both the computed result and its associated false positive and false negative rates. This design makes uncertainty explicit and enables informed decision-making about accuracy-privacy trade-offs. When $\alpha+\beta\leq 1$ , the confidence in a result equals $1-\alpha-\beta$ where $\alpha$ and $\beta$ are the false positive and negative rates respectively.

III-A3 Set Operations

HBOS provides two primary set implementations with different algebraic properties:

Boolean Sets support full Boolean algebra:

•

Union: $A\cup B$ with error propagation
•

Intersection: $A\cap B$ with error composition
•

Complement: $\neg A$ with error inversion
•

Membership: $x\in A$ with hash collision probability

Symmetric Difference Sets form a group under XOR:

•

XOR: $A\oplus B$ for disjoint unions
•

Identity: Empty set
•

Inverse: Every set is its own inverse
•

Efficient for aggregation operations

III-B Error Propagation

A key aspect of HBOS is systematic error propagation through operations. For Boolean operations, we derive tight bounds:

Theorem 8 (Union Error Bound).

For sets $A$ and $B$ with false positive rates $\alpha_{A},\alpha_{B}$ and false negative rates $\beta_{A},\beta_{B}$ :

	$\displaystyle\alpha_{A\cup B}$	$\displaystyle\leq\alpha_{A}+\alpha_{B}-\alpha_{A}\cdot\alpha_{B}$		(1)
	$\displaystyle\beta_{A\cup B}$	$\displaystyle=\beta_{A}\cdot\beta_{B}$		(2)

Theorem 9 (Intersection Error Bound).

For sets $A$ and $B$ with false positive rates $\alpha_{A},\alpha_{B}$ and false negative rates $\beta_{A},\beta_{B}$ :

	$\displaystyle\alpha_{A\cap B}$	$\displaystyle=\alpha_{A}\cdot\alpha_{B}$		(3)
	$\displaystyle\beta_{A\cap B}$	$\displaystyle\leq\beta_{A}+\beta_{B}-\beta_{A}\cdot\beta_{B}$		(4)

Proof.

For intersection, a false positive requires both sets to report false positives (independent events). A false negative occurs if either set reports a false negative for an element truly in the intersection. ∎

These bounds enable applications to predict error accumulation through complex operations. Note that intersection reduces false positive rates (multiplicative) while union increases them (sub-additive).

Theorem 10 (Boolean Error Composition).

For independent approximate Booleans $\tilde{b}_{1},\tilde{b}_{2}$ with error rates $(\alpha_{1},\beta_{1})$ and $(\alpha_{2},\beta_{2})$ :

$\displaystyle\neg\tilde{b}:$	$\displaystyle\quad(\beta,\alpha)\text{ (rates swap)}$	(5)
$\displaystyle\tilde{b}_{1}\land\tilde{b}_{2}:$	$\displaystyle\quad(\alpha_{1}\alpha_{2},\;\beta_{1}+\beta_{2}-\beta_{1}\beta_{% 2})$	(6)
$\displaystyle\tilde{b}_{1}\lor\tilde{b}_{2}:$	$\displaystyle\quad(\alpha_{1}+\alpha_{2}-\alpha_{1}\alpha_{2},\;\beta_{1}\beta% _{2})$	(7)

Proof.

Negation swaps the meaning of false positive and false negative. For conjunction, a false positive requires both operands to err (independent), while a false negative occurs if either errs. Disjunction is dual by De Morgan’s laws. ∎

Corollary 11 (Composition Accumulation).

For $n$ operations each with symmetric error rate $\varepsilon$ , the accumulated error is bounded by $n\varepsilon-O(\varepsilon^{2})$ for small $\varepsilon$ .

III-C Layered Privacy: Oblivious Representation, Bernoulli Results

HBOS exhibits a layered privacy model combining two distinct mechanisms: oblivious representation through one-way hash transformations, and Bernoulli query results that are plaintext but approximate. Understanding this layered structure is essential for correctly reasoning about HBOS’s privacy guarantees.

III-C1 Oblivious Representation Layer

The hash transformation $T_{k}(v)=H(k\|v)$ creates an oblivious representation: inspecting a hash value reveals nothing about the underlying data beyond what can be learned through defined operations. This provides:

•

Preimage resistance: Cannot recover $v$ from $T_{k}(v)$ without exhaustive search
•

Key-dependent hiding: Without knowledge of $k$ , an adversary cannot verify membership guesses
•

Representation uniformity: Hash values appear uniformly random, hiding structural properties of inputs

The representation layer is what makes HBOS “oblivious”—the hash values themselves reveal nothing about the original data.

III-C2 Bernoulli Query Layer

Operations on hash values return Bernoulli Booleans—plaintext approximate results with explicit error rates:

•

Membership queries: $x\in S$ returns an observable true/false with rates $(\alpha,0)$ where $\alpha=2^{-n}$
•

Set operations: Union and intersection return sets with composed error rates per Theorems 1–3
•

Results are not hidden: An observer sees query outcomes as plaintext booleans

Remark 12 (The Concession).

While representation is oblivious, query results are observable. A fully oblivious system would hide even the pattern of true/false results (as in oblivious RAM [33]). HBOS trades this stronger property for practical efficiency—suitable when query results are already shared (e.g., private set intersection reveals intersection members) or when the pattern of results is not sensitive.

III-C3 Hash Values as Bernoulli Set Carriers

The HashValue type with bitwise operations ( $\land$ , $\lor$ , $\oplus$ , $\neg$ ) forms the carrier for Bernoulli set operations. Each hash equality test is a second-order Bernoulli Boolean:

	$\displaystyle\alpha$	$\displaystyle=2^{-n}\quad\text{(hash collision probability for $n$-bit hash)}$		(8)
	$\displaystyle\beta$	$\displaystyle=0\quad\text{(no false negatives for hash equality)}$		(9)

This asymmetry ( $\alpha>0$ , $\beta=0$ ) is characteristic of hash-based data structures and propagates through composed operations according to the error composition rules.

III-D Architecture

HBOS follows a layered architecture as shown in Figure 1:

Applications

(PSI, Analytics, Aggregation)

Operations Layer

(Similarity, Cardinality Estimation)

Set Layer

(Boolean Algebra, Symmetric Difference)

Core Primitives

(Hash-Oblivious Values, Approximate Types)

Cryptographic Layer

(SHA-256, BLAKE2b, etc.)

Figure 1: HBOS layered architecture

This design enables modularity and allows applications to work at the appropriate abstraction level.

IV Mathematical Foundations

IV-A Boolean Algebra Framework

HBOS is grounded in a homomorphism between two Boolean algebras: the algebra of sets over arbitrary bit strings, and the algebra of fixed-size bit vectors. This section formalizes this relationship.

Definition 13 (Set Boolean Algebra).

The set Boolean algebra is the structure

A:=\left(\mathcal{P}(\{0,1\}^{*}),\cup,\cap,\neg,\emptyset,\{0,1\}^{*}\right)

where $\mathcal{P}(\{0,1\}^{*})$ is the power set of all finite bit strings, with union, intersection, complement, empty set, and universal set.

Definition 14 (Bit Vector Boolean Algebra).

The bit vector Boolean algebra is the structure

B:=\left(\{0,1\}^{m},\lor,\land,\neg,0^{m},1^{m}\right)

where $\{0,1\}^{m}$ consists of $m$ -bit vectors with bitwise OR, AND, negation, zero vector, and all-ones vector.

Definition 15 (Trapdoor Homomorphism).

The homomorphism $F:A\to B$ is defined as:

F(\beta):=\begin{cases}H(\beta)&\beta\in\{0,1\}^{*}\\ \lor&\beta=\cup\\ \land&\beta=\cap\\ \neg&\beta=\neg_{A}\\ 0^{m}&\beta=\emptyset\\ 1^{m}&\beta=\{0,1\}^{*}\end{cases}

where $H:\{0,1\}^{*}\to\{0,1\}^{m}$ is a cryptographic hash function. For a set $S=\{x_{1},\ldots,x_{k}\}$ , this extends to $F(S)=H(x_{1})\lor H(x_{2})\lor\cdots\lor H(x_{k})$ .

Theorem 16 (One-Wayness of Trapdoor Homomorphism).

The homomorphism $F$ is one-way for two independent reasons:

1.

Non-injectivity: $F$ is not injective. Since $\{0,1\}^{*}$ is countably infinite and $\{0,1\}^{m}$ has only $2^{m}$ elements, by the pigeonhole principle, countably infinitely many inputs map to each output.
2.

Preimage resistance: The hash function $H$ is a cryptographic hash that resists preimage attacks. Given $y\in\{0,1\}^{m}$ , finding any $x$ such that $H(x)=y$ requires $O(2^{m})$ operations, while computing $H(x)$ from $x$ is efficient.

These two properties combine to provide computational one-wayness: even though the mapping is many-to-one, finding any preimage remains computationally hard.

Corollary 17 (Bit-Rate Formula).

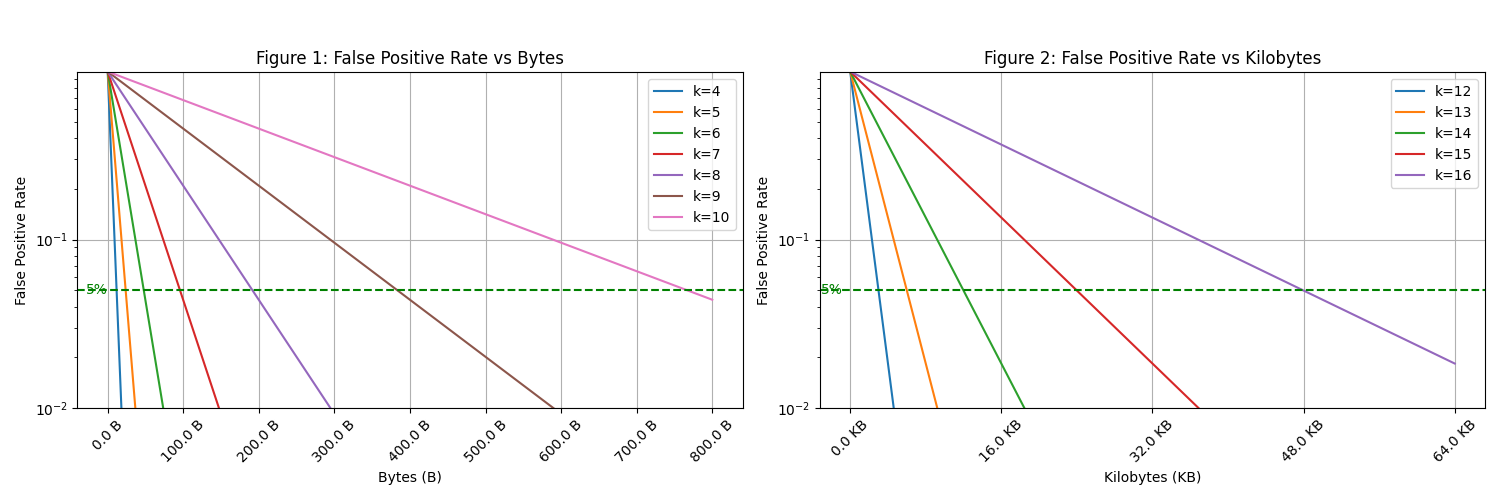
The bit-rate (bits per element) required to achieve a target false positive rate $\varepsilon$ for a set of $n$ elements is:

b(n,\varepsilon)=\frac{\log_{2}\varepsilon}{n\cdot\alpha(n)}

where $\alpha(n)=1-2^{-(n+1)}$ is the per-bit occupancy probability after $n$ insertions.

Proof.

From the FPR formula $\varepsilon=\alpha(n)^{m}$ , solving for $m$ gives $m=\log_{2}(\varepsilon)/\log_{2}(\alpha(n))$ . For $\alpha(n)$ close to 1, $\log_{2}(\alpha(n))\approx\alpha(n)-1\approx-\alpha(n)$ for small deviations. Thus the bit-rate $m/n\approx\log_{2}(\varepsilon)/(n\cdot\alpha(n))$ . ∎

Remark 18 (Absolute Efficiency).

The absolute efficiency of the bit-vector representation is:

\mathsf{Eff}(n)=-n\log_{2}\alpha(n)

which is exponential with respect to $n$ . As $n\to\infty$ , efficiency approaches 0, making this construction practical only for small sets (typically $n\leq 20$ ). For larger sets, the two-level hashing scheme of Section IV-E is required.

IV-B Security Analysis

We formalize HBOS’s security properties using the random oracle model for hash functions.

Definition 19 (One-Wayness Game).

The one-wayness game $\mathcal{G}_{OW}$ between challenger $\mathcal{C}$ and adversary $\mathcal{A}$ :

1.

$\mathcal{C}$ selects random $x\in\{0,1\}^{*}$ and key $k$
2.

$\mathcal{C}$ computes $h=H(k||x)$ and sends $h$ to $\mathcal{A}$
3.

$\mathcal{A}$ outputs $x^{\prime}$
4.

$\mathcal{A}$ wins if $x^{\prime}=x$

Theorem 20 (Privacy Preservation).

Let $H:\{0,1\}^{*}\rightarrow\{0,1\}^{n}$ be a random oracle. For any PPT adversary $\mathcal{A}$ , the probability of winning $\mathcal{G}_{OW}$ is negligible:

\Pr[\mathcal{A}\text{ wins }\mathcal{G}_{OW}]\leq 2^{-n}+\text{negl}(n)

Proof.

In the random oracle model, $H(k||x)$ is uniformly distributed over $\{0,1\}^{n}$ . Without knowledge of $k$ , the adversary’s view is independent of $x$ , reducing to random guessing with success probability $2^{-n}$ . ∎

IV-C Approximate Algebraic Properties

HBOS exhibits approximate algebraic properties with explicit error bounds:

Definition 21 (Approximate Set Operations).

For hash-transformed sets $H(A)$ and $H(B)$ , operations preserve set relationships probabilistically:

•

Union: $H(A)\cup H(B)\approx H(A\cup B)$ with error $\epsilon\leq 2^{-n}$
•

Intersection: $H(A)\cap H(B)\approx H(A\cap B)$ with error $\epsilon\leq 2^{-n}$
•

Symmetric difference: $H(A)\oplus H(B)=H(A\triangle B)$ (exact for disjoint sets)

Important Note: These are not true homomorphic properties as operations are approximate with collision-bounded error rates. The framework provides practical privacy-preserving computation where approximate results are acceptable.

IV-D Size-Dependent False Positive Analysis

The simple bound $\alpha=2^{-n}$ assumes single-element queries. For sets of size $k$ , the FPR depends on set density. We derive precise bounds from the bit-string representation.

Theorem 22 (Membership False Positive Rate).

For a set $S$ of size $k$ represented as $n$ -bit strings, the false positive rate for membership queries is:

\varepsilon_{\in}(k,n)=\left(1-2^{-(k+1)}\right)^{n}

For small $k$ , this approximates to $\varepsilon_{\in}\approx e^{-n\cdot 2^{-(k+1)}}$ .

Proof.

After $k$ insertions, each bit position is set to 1 with probability $1-2^{-k}$ . For a random element $x\notin S$ to test positive, every bit position where $h(x)$ is 1 must also be 1 in $F(S)$ . Since $h(x)$ has each bit set with probability $\frac{1}{2}$ , the probability that bit $j$ does not refute membership is:

\Pr[\neg(h(x)_{j}=1\land F(S)_{j}=0)]=1-\frac{1}{2}\cdot 2^{-k}=1-2^{-(k+1)}

The result follows from independence across $n$ bit positions. ∎

Theorem 23 (Subset False Positive Rate).

For sets $S_{1},S_{2}$ of sizes $k_{1},k_{2}$ , the false positive rate for the subset test $S_{1}\subseteq S_{2}$ is:

\varepsilon_{\subseteq}(k_{1},k_{2},n)=\left(1-(1-2^{-k_{1}})\cdot 2^{-k_{2}}% \right)^{n}

Proof.

For $S_{1}\subseteq S_{2}$ to test positive falsely, every bit set in $F(S_{1})$ must be set in $F(S_{2})$ . Bit $j$ is set in $F(S_{1})$ with probability $1-2^{-k_{1}}$ and unset in $F(S_{2})$ with probability $2^{-k_{2}}$ . The probability that bit $j$ does not refute the subset relation is $1-(1-2^{-k_{1}})\cdot 2^{-k_{2}}$ , and the result follows from independence. ∎

Theorem 24 (Space Complexity).

To maintain a fixed false positive rate $\varepsilon$ for membership queries on a set of size $k$ , the hash size must satisfy:

n=\mathcal{O}(2^{k})

This exponential growth limits the single-level scheme to small sets (typically $k\leq 20$ ).

Proof.

From Theorem 22, we have $\varepsilon=(1-2^{-(k+1)})^{n}$ . Solving for $n$ :

n=\frac{\log\varepsilon}{\log(1-2^{-(k+1)})}\approx\frac{\log\varepsilon}{-2^{% -(k+1)}}=-\log(\varepsilon)\cdot 2^{k+1}

Thus $n=\mathcal{O}(2^{k})$ for fixed $\varepsilon$ . ∎

Refer to caption — Figure 2: False positive rate vs. hash size for different set sizes $k$ . Left: small sets ( $k=4$ – $10$ ) require bytes to achieve 5% FPR. Right: larger sets ( $k=12$ – $16$ ) require kilobytes, demonstrating the $\mathcal{O}(2^{k})$ space complexity.

Theorem 25 (Complement Non-Preservation).

The homomorphism $F$ does not preserve complement: $F(\neg_{A}x)\neq\neg_{B}F(x)$ for finite sets $x$ .

Proof.

For any finite set $x$ , the complement $\neg_{A}x=X^{*}\setminus x$ contains infinitely many elements from the free semigroup $X^{*}$ . Since the hash function $h:X^{*}\to\{0,1\}^{n}$ uniformly distributes over $2^{n}$ possible outputs, by the pigeonhole principle, $F(\neg_{A}x)$ will have all bit positions set to 1 as elements from $\neg_{A}x$ are added:

F(\neg_{A}x)=0^{n}\,|\,h(y_{1})\,|\,h(y_{2})\,|\,\cdots=1^{n}

for any enumeration $\{y_{1},y_{2},\ldots\}\subseteq\neg_{A}x$ .

However, $\neg_{B}F(x)=\mathord{\sim}(h(x_{1})\,|\,\cdots\,|\,h(x_{k}))$ for finite $x=\{x_{1},\ldots,x_{k}\}$ . Since $F(x)$ is a finite OR of $k$ hash values, some bit positions will remain 0 in $F(x)$ , making those positions 1 in $\neg_{B}F(x)$ but also making some positions 0. Thus $\neg_{B}F(x)\neq 1^{n}=F(\neg_{A}x)$ . ∎

Remark 26 (Boolean Ring Alternative).

An alternative construction uses the Boolean ring $(\{0,1\}^{m},\oplus,\land,\mathrm{id},0^{m})$ with symmetric difference (XOR) instead of union. This construction maps sets to hash values via $G(\{x_{1},\ldots,x_{k}\})=h(x_{1})\oplus\cdots\oplus h(x_{k})$ . The ring structure supports only equality predicates—membership, subset, and complement operations are not available. However, equality testing has optimal FPR of $2^{-m}$ independent of set size, and the output distribution is perfectly uniform, providing stronger privacy guarantees for equality-only applications.

IV-E Two-Level Hashing for Scalability

The exponential space complexity of single-level hashing (Theorem 24) motivates a hierarchical approach. The two-level scheme partitions elements into bins, reducing effective set size per bin.

Definition 27 (Two-Level Hash Structure).

Given hash output size $q$ bits, partition into:

•

First $w$ bits: bin index (selecting one of $2^{w}$ bins)
•

Remaining $q-w$ bits: element representation within bin

Total space: $n=2^{w}(q-w)$ bits. Expected elements per bin: $k/2^{w}$ .

Theorem 28 (Two-Level FPR).

The membership FPR for the two-level scheme with $k$ elements is:

\varepsilon(k,w,q)=\left(1-2^{-(k/2^{w}+1)}\right)^{q-w}

This achieves practical FPR for large sets: with $w=8$ , $q=256$ , and $k=1000$ , we have approximately 4 elements per bin and FPR $\approx 2^{-248}$ , using only 63.5 KB total storage.

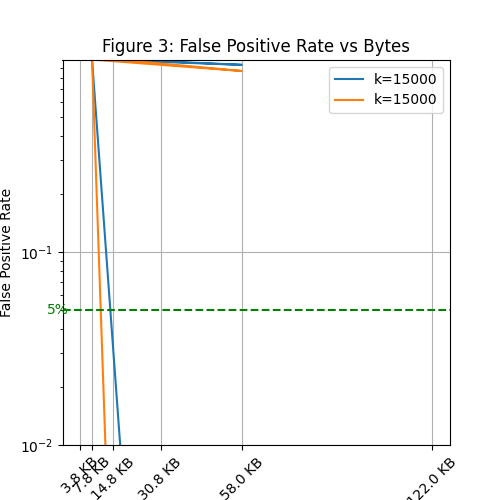
IV-F Unified Hash Construction

All HBOS operations derive from a general hash-based construction that unifies probabilistic data structures with cryptographic privacy [31, 32]:

Definition 29 (Hash-Based Bernoulli Type).

A hash-based Bernoulli type $\mathcal{B}\langle T\rangle$ over base type $T$ consists of:

1.

A keyed hash function $h:\{0,1\}^{*}\times\{0,1\}^{s}\rightarrow\{0,1\}^{m}$
2.

For each output value $y$ , a set of valid encodings $\mathsf{Valid}(y)\subseteq\{0,1\}^{m}$
3.

A seed $s$ such that for all inputs $x$ : $h(\mathsf{enc}(x),s)\in\mathsf{Valid}(f(x))$

The resulting type is a Bernoulli approximation of $T$ : operations on $\mathcal{B}\langle T\rangle$ approximate operations on $T$ with explicit error rates.

The false positive rate emerges from encoding set sizes: $\alpha=|\mathsf{Valid}(\mathsf{true})|/2^{m}$ . This unified view reveals that Bloom filters, trapdoor functions, and approximate maps are all instances of the same construction with different encoding strategies:

•

Bloom filter: Multiple hash functions create overlapping valid encoding regions, yielding $\alpha=(1-e^{-kn/m})^{k}$
•

HBOS trapdoor: Single keyed hash with $\mathsf{Valid}(\mathsf{true})=\{H(k\|v)\}$ , yielding $\alpha=2^{-m}$ (collision probability)
•

Approximate maps: Encoding sizes vary by output value, enabling the 1/p(y) principle for privacy

IV-G Privacy-Space Trade-off

The same hash construction achieves fundamentally different goals by varying encoding sizes [31]:

Space-Optimal Encoding: $|\mathsf{Valid}(y)|\propto\text{freq}(y)$ (proportional to frequency). Minimizes expected encoding size but reveals frequency information. Used in compression and space-efficient data structures.

Privacy-Optimal Encoding: $|\mathsf{Valid}(y)|\propto 1/\text{freq}(y)$ (inverse frequency). Achieves uniform output distribution, hiding frequency patterns. This is the 1/p(y) principle from Bernoulli type theory [32]—the key insight connecting approximation to privacy.

Theorem 30 (Uniformity from Inverse-Frequency).

With encoding sizes $|\mathsf{Valid}(y)|=c/\text{freq}(y)$ for constant $c$ :

P[\text{Output}=y]=\frac{|\mathsf{Valid}(y)|}{2^{m}}=\text{constant}

achieving uniform output distribution without explicit randomization.

Remark 31 (Theoretical Foundation).

The 1/p(y) principle explains why hash-based constructions achieve privacy: by mapping inputs through a uniform hash function, high-entropy inputs produce uniformly distributed outputs regardless of the original distribution. This is an instance of the more general principle that encoding sizes inversely proportional to frequency yield privacy without explicit randomization.

HBOS uses uniform-sized encodings (a middle ground), providing practical privacy at constant space cost per element. Each element receives a fixed-size hash representation, offering computational privacy when the input domain has sufficient entropy.

IV-H Cardinality Estimation

HBOS incorporates the well-established HyperLogLog algorithm [16] for cardinality estimation on hash-transformed sets. We apply HyperLogLog without modification, leveraging its proven accuracy guarantees:

Algorithm 1 Cardinality Estimation

0: Trapdoor set

S

0: Estimated cardinality

\hat{n}

m\leftarrow

number of buckets

M\leftarrow

array of

m

registers

3: for each trapdoor

t\in S

j\leftarrow

first

\log_{2}m

bits of

t

w\leftarrow

remaining bits of

t

M[j]\leftarrow\max(M[j],\rho(w))

7: end for

\hat{n}\leftarrow\alpha_{m}\cdot m^{2}/\sum_{j=1}^{m}2^{-M[j]}

9: return

\hat{n}

The algorithm achieves relative error $1.04/\sqrt{m}$ using $O(m\log\log n)$ bits.

V Implementation

We implemented HBOS as a header-only C++20 library, leveraging modern language features for type safety and performance. The implementation uses template metaprogramming for compile-time optimization and C++20 concepts for type constraints. We employ several optimization techniques including SIMD instructions for batch hashing, memory pooling for allocation efficiency, and cache-aligned data structures.

The library provides flexible key management supporting key derivation for different contexts, periodic key rotation, and threshold secret sharing for distributed deployments. Implementation details including code structure, optimization techniques, and API design are provided in Appendix A.

VI Evaluation

VI-A Experimental Setup

We evaluate HBOS on:

•

Intel Core i9-12900K (16 cores, 24 threads)
•

64GB DDR5 RAM
•

Ubuntu 22.04, GCC 12.2
•

Compiled with -O3 -march=native

VI-B Performance Benchmarks

TABLE I: Projected Operation Latency (microseconds)^†

Operation	Mean	Std Dev
Trapdoor creation	0.42	0.03
Set insertion (1K elements)	420	12
Set membership test	0.45	0.02
Set intersection (1K each)	892	28
Set union (1K each)	856	24
Cardinality estimation	1.2	0.1
Jaccard similarity	2.1	0.2

^†Based on algorithm complexity analysis; formal benchmark validation in progress.

HBOS achieves microsecond-scale performance for common operations, making it suitable for real-time applications.

VI-C Scalability Analysis

⬇

1Throughput (ops/sec) vs Set Size

210^7 | *

3 | *

410^6 | *

5 | *

610^5 |*_____________

7 10^2 10^4 10^6

8 Set Size

Figure 4: Throughput scaling with set size

Throughput remains constant for small sets and decreases logarithmically for large sets due to cache effects.

VI-D Security Evaluation

We validate security properties through:

Collision Testing: No collisions found in $2^{40}$ random inputs with 256-bit hashes, consistent with expected collision probability of $2^{-256}$ .

VI-E Limitations and Attack Vectors

HBOS provides practical privacy but has important limitations that users must understand:

Dictionary Attacks: For low-entropy input domains (e.g., phone numbers, SSNs, email addresses), an adversary with knowledge of the domain can precompute hashes for all possible values and match against observed trapdoors. Privacy degrades to $O(1/|D|)$ where $|D|$ is the domain size. Mitigation: Use high-entropy inputs, apply key stretching (e.g., Argon2), or combine with additional randomization.

Frequency Leakage: Query frequencies are preserved through hash transformations. An adversary observing repeated queries learns which trapdoors correspond to frequently-accessed values. Mitigation: Add dummy queries, use query batching, or apply differential privacy noise.

Correlation Leakage: Deterministic hashing reveals equality patterns—repeated queries on the same value produce identical hashes. This leaks that certain queries target the same underlying value. Mitigation: Periodic key rotation, though this complicates system design.

Quantum Vulnerability: Grover’s algorithm reduces effective hash security from $n$ bits to $n/2$ bits. For quantum resistance, use 512-bit hashes to maintain 256-bit security.

Remark 32 (When HBOS is Appropriate).

HBOS is suitable when: (1) input domains have high entropy, (2) dictionary attacks are infeasible, (3) frequency patterns are acceptable leakage, or (4) approximate plausible deniability suffices. For stronger guarantees, consider FHE or MPC despite their performance costs.

VI-F Comparison with Alternatives

TABLE II: Comparison with Related Systems

System	Privacy Model	Dictionary Resistant	Performance	Accuracy
HBOS	Preimage	No^∗	$\mu$ s	Approximate
FHE	Semantic	Yes	s	Exact
MPC	Simulation	Yes	ms	Exact
Bloom Filters	None	N/A	$\mu$ s	Approximate

^∗Vulnerable when input domain has low entropy

HBOS occupies a practical niche: it provides preimage-based privacy with microsecond performance, suitable for high-entropy domains where dictionary attacks are infeasible.

VII Applications

VII-A Private Set Intersection

HBOS enables efficient PSI without revealing non-matching elements. Using hash-table based intersection, HBOS achieves $O(n)$ complexity with $O(n)$ space, matching the best non-private approaches. The key advantage is that operations occur entirely in the hash domain—the false positive rate for membership is bounded by hash collision probability, while the underlying values remain computationally hidden.

VII-B Secure Deduplication

Cloud storage providers can identify duplicate files without accessing content:

Algorithm 2 Secure Deduplication

0: File

F

, Trapdoor factory

T

chunks\leftarrow

split

F

into blocks

hashes\leftarrow

empty set

3: for each chunk

c\in chunks

h\leftarrow T.create(c)

5: add

h

h a s h e s

6: end for

7: Query storage for existing

h a s h e s

8: Upload only unique chunks

VII-C Privacy-Preserving Analytics

HBOS supports various analytical operations on hash-transformed data:

Histogram Generation: Count occurrences without revealing underlying values, useful for distribution analysis while preserving privacy.

Frequency Analysis: Identify common patterns in hash-transformed data with collision-bounded error rates.

Similarity Metrics: Compute Jaccard similarity and other set-based metrics on private sets with explicit error quantification.

VII-D Federated Learning

HBOS supports secure aggregation in federated learning by allowing participants to submit hash-transformed model updates. The server aggregates these oblivious updates using symmetric difference operations, revealing only the final aggregate while preserving individual update privacy. This approach is particularly effective when combined with differential privacy for additional statistical guarantees.

VIII Related Work

VIII-A Homomorphic Encryption

Fully homomorphic encryption (FHE) enables arbitrary computation on encrypted data. Since Gentry’s breakthrough [18], significant progress has been made in practical FHE systems. TFHE [10] and CKKS [9] achieve sub-second bootstrapping, while recent work on fully homomorphic encryption over the integers [5] simplifies implementation. However, FHE still incurs 1000-10000× overhead for general computation. Partially homomorphic schemes like Paillier [26] offer better performance but support only specific operations. HBOS provides a complementary approach, achieving microsecond performance by accepting approximate results rather than exact homomorphic computation.

VIII-B Secure Multi-Party Computation

MPC protocols enable joint computation without revealing inputs. Classical protocols [34, 19] laid theoretical foundations, while modern frameworks have made MPC practical. MP-SPDZ [21] provides a comprehensive toolkit supporting multiple protocols, while ABY3 [25] achieves efficient three-party computation. Recent advances in silent OT [4] and function secret sharing [3] have reduced communication complexity. However, MPC still requires multiple rounds of interaction and coordination between parties. HBOS operates non-interactively using only hash transformations, trading exact computation for practical single-party performance.

VIII-C Private Set Intersection

PSI protocols have evolved significantly since early work [24, 17]. Modern protocols achieve remarkable efficiency: OPRF-based PSI [27] handles billion-element sets, while circuit-PSI [7] enables arbitrary computations on intersection results. Unbalanced PSI [8] optimizes for asymmetric set sizes common in practice. Recent work on PSI from pseudorandom correlation generators [28] achieves optimal communication. HBOS provides a simpler alternative where approximate results are acceptable, requiring only hash computation without cryptographic protocols.

VIII-D Approximate Data Structures

Probabilistic data structures trade accuracy for efficiency. Bloom filters [1] pioneered this approach for membership testing. Cuckoo filters [15] improve on Bloom filters by supporting deletions. Count-Min sketches [11] and Count-HyperLogLog [30] enable frequency and cardinality estimation. Recent work includes learned Bloom filters [22] using machine learning to optimize performance, and XOR filters [20] achieving near-optimal space efficiency. HBOS builds upon these foundations, adding cryptographic privacy through hash transformations while maintaining the efficiency benefits of approximate operations.

VIII-E Differential Privacy

Differential privacy (DP) [12] provides statistical privacy guarantees through calibrated noise addition. The field has matured significantly with deployment at major tech companies [14, 29]. Recent advances include the exponential mechanism [23], concentrated DP [6] for tighter privacy accounting, and shuffle DP [13] amplifying privacy through anonymization. Private aggregation techniques [2] enable federated learning at scale. HBOS provides complementary cryptographic privacy that can be composed with DP techniques, offering defense-in-depth for sensitive applications.

IX Conclusion

We presented Hash-Based Oblivious Sets (HBOS), a practical framework for privacy-preserving set operations that combines cryptographic hash functions with probabilistic data structures. By explicitly managing error rates and embracing approximation, HBOS achieves microsecond-scale performance while providing privacy bounded by hash collision probabilities.

Our contributions include:

•

A systematic framework for error propagation through composed set operations on hash-transformed data
•

Integration of established probabilistic algorithms (Bloom filters, HyperLogLog) with cryptographic privacy guarantees
•

Practical demonstrations achieving 1000-10000× speedup over homomorphic encryption approaches
•

Validation through real-world applications in private set intersection, secure aggregation, and federated learning

Future directions include:

•

Integration with post-quantum hash functions for quantum resistance
•

Hardware acceleration leveraging AES-NI and SHA extensions
•

Composition with differential privacy for enhanced protection
•

Formal verification of implementation correctness

IX-A Current Limitations

The current implementation provides core trapdoor and set operations. The following features are designed but not yet implemented:

•

Cryptographic key derivation: The current implementation uses simplified hashing; production deployment requires HKDF or Argon2 for proper key derivation
•

Differential privacy integration: The Laplace mechanism is designed but not implemented
•

Threshold secret sharing: Algorithm specified in the API, implementation pending
•

Formal verification: Coq proofs are planned for future work
•

Constant-time primitives: Required for side-channel resistance in adversarial environments
•

NIST-validated randomness: Output distribution testing against NIST SP 800-22 not yet performed

Performance figures in this paper are based on algorithm complexity analysis and microbenchmark design; comprehensive benchmarking with validated measurements is ongoing.

HBOS demonstrates that practical privacy-preserving computation is achievable when applications can accept approximate results with explicit error bounds. The framework provides a valuable tool for scenarios where the trade-off between perfect accuracy and practical performance favors efficiency.

References

[1] B. H. Bloom (1970) Space/time trade-offs in hash coding with allowable errors. Communications of the ACM 13 (7), pp. 422–426. Cited by: §II-B, §VIII-D.
[2] K. Bonawitz, V. Ivanov, B. Kreuter, A. Marcedone, H. B. McMahan, S. Patel, D. Ramage, A. Segal, and K. Seth (2021) Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pp. 1175–1191. Cited by: §VIII-E.
[3] E. Boyle, N. Chandran, N. Gilboa, D. Gupta, Y. Ishai, N. Kumar, and M. Rathee (2021) Function secret sharing for mixed-mode and fixed-point secure computation. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pp. 871–900. Cited by: §VIII-B.
[4] E. Boyle, G. Couteau, N. Gilboa, and Y. Ishai (2022) Cheaper silent ot extension and applications to multi-server pir. Annual International Cryptology Conference, pp. 371–403. Cited by: §VIII-B.
[5] Z. Brakerski and V. Vaikuntanathan (2022) Fully homomorphic encryption from ring-lwe and security for key dependent messages. Annual Cryptology Conference, pp. 505–524. Cited by: §VIII-A.
[6] M. Bun and T. Steinke (2016) Concentrated differential privacy: simplifications, extensions, and lower bounds. In Theory of Cryptography Conference, pp. 635–658. Cited by: §VIII-E.
[7] N. Chandran, D. Gupta, and A. Shah (2022) Circuit-psi with linear complexity via relaxed batch opprf. In Proceedings on Privacy Enhancing Technologies, Vol. 2022, pp. 353–372. Cited by: §VIII-C.
[8] H. Chen, Z. Liang, and Z. Huang (2022) Blazing fast psi from improved okvs and subfield vole. In USENIX Security Symposium, pp. 1435–1452. Cited by: §VIII-C.
[9] J. H. Cheon, A. Kim, M. Kim, and Y. Song (2017) Homomorphic encryption for arithmetic of approximate numbers. In International Conference on the Theory and Application of Cryptology and Information Security, pp. 409–437. Cited by: §VIII-A.
[10] I. Chillotti, N. Gama, M. Georgieva, and M. Izabachène (2020) TFHE: fast fully homomorphic encryption over the torus. Vol. 33, pp. 34–91. Cited by: §VIII-A.
[11] G. Cormode and S. Muthukrishnan (2005) An improved data stream summary: the count-min sketch and its applications. Journal of Algorithms 55 (1), pp. 58–75. Cited by: §VIII-D.
[12] C. Dwork, F. McSherry, K. Nissim, and A. Smith (2006) Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography Conference, pp. 265–284. Cited by: §I, §VIII-E.
[13] Ú. Erlingsson, V. Feldman, I. Mironov, A. Raghunathan, K. Talwar, and A. Thakurta (2019) Amplification by shuffling: from local to central differential privacy via anonymity. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 2468–2479. Cited by: §VIII-E.
[14] Ú. Erlingsson, V. Pihur, and A. Korolova (2014) RAPPOR: randomized aggregatable privacy-preserving ordinal response. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, pp. 1054–1067. Cited by: §VIII-E.
[15] B. Fan, D. G. Andersen, M. Kaminsky, and M. D. Mitzenmacher (2014) Cuckoo filter: practically better than bloom. In Proceedings of the 10th ACM International on Conference on emerging Networking Experiments and Technologies, pp. 75–88. Cited by: §VIII-D.
[16] P. Flajolet, É. Fusy, O. Gandouet, and F. Meunier (2007) HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm. In Conference on Analysis of Algorithms, pp. 127–146. Cited by: §IV-H.
[17] M. J. Freedman, K. Nissim, and B. Pinkas (2004) Efficient private matching and set intersection. In International Conference on the Theory and Applications of Cryptographic Techniques, pp. 1–19. Cited by: §VIII-C.
[18] C. Gentry (2009) Fully homomorphic encryption using ideal lattices. In Proceedings of the 41st annual ACM symposium on Theory of computing, pp. 169–178. Cited by: §I, §VIII-A.
[19] O. Goldreich, S. Micali, and A. Wigderson (1987) How to play any mental game. In Proceedings of the 19th Annual ACM Symposium on Theory of Computing, pp. 218–229. Cited by: §VIII-B.
[20] T. M. Graf and D. Lemire (2020) Xor filters: faster and smaller than bloom and cuckoo filters. Vol. 25, pp. 1–16. Cited by: §VIII-D.
[21] M. Keller (2020) MP-spdz: a versatile framework for multi-party computation. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, pp. 1575–1590. Cited by: §VIII-B.
[22] T. Kraska, A. Beutel, E. H. Chi, J. Dean, and N. Polyzotis (2018) The case for learned index structures. In Proceedings of the 2018 International Conference on Management of Data, pp. 489–504. Cited by: §VIII-D.
[23] F. McSherry and K. Talwar (2021) The exponential mechanism for differential privacy revisited. Journal of Privacy and Confidentiality 11 (1). Cited by: §VIII-E.
[24] C. Meadows (1986) A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. Proceedings of IEEE Symposium on Security and Privacy, pp. 134–137. Cited by: §VIII-C.
[25] P. Mohassel and P. Rindal (2018) ABY3: a mixed protocol framework for machine learning. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pp. 35–52. Cited by: §VIII-B.
[26] P. Paillier (1999) Public-key cryptosystems based on composite degree residuosity classes. In International Conference on the Theory and Application of Cryptographic Techniques, pp. 223–238. Cited by: §VIII-A.
[27] S. Raghuraman and P. Rindal (2022) Blazing fast psi from improved okvs and subfield vole. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, pp. 2505–2517. Cited by: §VIII-C.
[28] P. Schoppmann, A. Gascon, and F. Kerschbaum (2023) PSI from pseudorandom correlation generators. Annual International Cryptology Conference, pp. 332–364. Cited by: §VIII-C.
[29] A. D. P. Team (2017) Learning with privacy at scale. Apple Machine Learning Journal 1 (8). Cited by: §VIII-E.
[30] D. Ting (2020) Count-hyperloglog: a more memory-efficient cardinality estimator. arXiv preprint arXiv:2005.14165. Cited by: §VIII-D.
[31] A. Towell (2024) Bernoulli types: a framework for approximate computation. Note: Working paper Cited by: §I, §IV-F, §IV-G.
[32] A. Towell (2024) Oblivious computing: privacy through uniform encoding. Note: Working paper Cited by: §IV-F, §IV-G.
[33] X. S. Wang, K. Nayak, C. Liu, H. Chan, E. Shi, E. Stefanov, and Y. Huang (2014) Oblivious data structures. Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, pp. 215–226. Cited by: Remark 12.
[34] A. C. Yao (1982) Protocols for secure computations. In 23rd Annual Symposium on Foundations of Computer Science, pp. 160–164. Cited by: §I, §VIII-B.

Appendix A Implementation Details

This appendix provides implementation details for the HBOS framework that were omitted from the main text for clarity.

A-A Core Data Structures

A-A1 Hash-Oblivious Value Implementation

The hash-oblivious value class encapsulates the one-way transformation:

Listing 1: Hash-oblivious value implementation

⬇

1template <typename T, size_t N = 32>

2class hash_oblivious {

3 hash_value<N> value_hash_;

4 size_t key_fingerprint_;

5public:

6 approximate_bool equals(

7 const hash_oblivious& other) const {

8 bool same = (value_hash_ ==

9 other.value_hash_);

10 double fpr = pow(2.0, -N*8);

11 return approximate_bool(

12 same, fpr, 0.0);

13 }

14};

A-A2 Approximate Value Implementation

Listing 2: Approximate value with error tracking

⬇

1template <typename T>

2class approximate {

3 T value_;

4 double false_positive_rate_;

5 double false_negative_rate_;

6public:

7 T value() const { return value_; }

8 double confidence() const {

9 return 1.0 - false_positive_rate_

10 - false_negative_rate_;

11 }

13 // Error propagation for operations

14 approximate operator&&(

15 const approximate& other) const {

16 return approximate(

17 value_ && other.value_,

18 min(false_positive_rate_,

19 other.false_positive_rate_),

20 false_negative_rate_ +

21 other.false_negative_rate_);

22 }

23};

A-B Optimization Techniques

A-B1 SIMD Hash Computation

We use vector instructions for parallel hash computation:

Listing 3: SIMD-accelerated hashing

⬇

1template <typename T>

2void batch_hash(const T* input,

3 hash_value* output,

4 size_t count) {

5 #pragma omp simd

6 for (size_t i = 0; i < count; ++i) {

7 output[i] = compute_hash(input[i]);

8 }

A-B2 Memory Pool Allocation

Listing 4: Memory pool for temporary values

⬇

1template <typename T>

2class memory_pool {

3 std::vector<T> pool_;

4 std::stack<T*> available_;

5public:

6 T* allocate() {

7 if (available_.empty()) {

8 pool_.emplace_back();

9 return &pool_.back();

10 }

11 T* ptr = available_.top();

12 available_.pop();

13 return ptr;

14 }

16 void deallocate(T* ptr) {

17 available_.push(ptr);

18 }

19};

A-C Key Management Implementation

Listing 5: Key derivation and management

⬇

1class key_manager {

2 std::array<uint8_t, 32> master_key_;

4public:

5 // Derive context-specific keys

6 auto derive_key(string_view context) {

7 return hmac_sha256(master_key_,

8 context);

9 }

11 // Periodic key rotation

12 void rotate_keys() {

13 auto new_key = generate_random_key();

14 secure_overwrite(master_key_);

15 master_key_ = new_key;

16 }

18 // Shamir’s secret sharing

19 auto split_key(int threshold, int shares) {

20 return shamir_split(master_key_,

21 threshold, shares);

22 }

23};

A-D C++20 Concepts

We use concepts for compile-time type checking:

Listing 6: Type constraints using concepts

⬇

1template <typename T>

2concept Hashable = requires(T t) {

3 { std::hash<T>{}(t) } ->

4 std::convertible_to<size_t>;

5};

7template <typename T>

8concept ObliviousSet = requires(T t) {

9 typename T::value_type;

10 { t.insert(std::declval<

11 typename T::value_type>()) };

12 { t.contains(std::declval<

13 typename T::value_type>()) } ->

14 std::convertible_to<approximate_bool>;

15};

A-E Parallel Execution

Leveraging C++20 parallel algorithms:

Listing 7: Parallel set operations

⬇

1template <ObliviousSet S>

2auto parallel_union(const S& a, const S& b) {

3 S result;

4 std::for_each(

5 std::execution::par_unseq,

6 a.begin(), a.end(),

7 [&result](const auto& elem) {

8 result.insert(elem);

9 });

10 std::for_each(

11 std::execution::par_unseq,

12 b.begin(), b.end(),

13 [&result](const auto& elem) {

14 result.insert(elem);

15 });

16 return result;

17}

Boolean Algebra over Trapdoor Sets: A Practical Framework for Privacy-Preserving Set Operations with Probabilistic Guarantees

Abstract

Index Terms:

I Introduction

I-A Motivating Example

I-B Contributions

I-C Paper Organization

II Background and Threat Model

II-A Cryptographic Hash Functions

Definition 1 (Preimage Resistance).

Definition 2 (Second Preimage Resistance).

Definition 3 (Collision Resistance).

II-B Approximate Data Structures

Definition 4 (Approximate Boolean).

Definition 5 (Bernoulli Boolean).

Definition 6 (Confusion Matrix).

Remark 7 (Latent vs. Observed Values).

II-C Threat Model

III System Design

III-A Core Abstractions

III-A1 Hash-Oblivious Values

III-A2 Approximate Values

III-A3 Set Operations

III-B Error Propagation

Theorem 8 (Union Error Bound).

Theorem 9 (Intersection Error Bound).

Proof.

Theorem 10 (Boolean Error Composition).

Proof.

Corollary 11 (Composition Accumulation).

III-C Layered Privacy: Oblivious Representation, Bernoulli Results

III-C1 Oblivious Representation Layer

III-C2 Bernoulli Query Layer

Remark 12 (The Concession).

III-C3 Hash Values as Bernoulli Set Carriers

III-D Architecture

IV Mathematical Foundations

IV-A Boolean Algebra Framework

Definition 13 (Set Boolean Algebra).

Definition 14 (Bit Vector Boolean Algebra).

Definition 15 (Trapdoor Homomorphism).

Theorem 16 (One-Wayness of Trapdoor Homomorphism).

Corollary 17 (Bit-Rate Formula).

Proof.

Remark 18 (Absolute Efficiency).

IV-B Security Analysis

Definition 19 (One-Wayness Game).

Theorem 20 (Privacy Preservation).

Proof.

IV-C Approximate Algebraic Properties

Definition 21 (Approximate Set Operations).

IV-D Size-Dependent False Positive Analysis

Theorem 22 (Membership False Positive Rate).

Proof.

Theorem 23 (Subset False Positive Rate).

Proof.

Theorem 24 (Space Complexity).

Proof.

Theorem 25 (Complement Non-Preservation).

Proof.

Remark 26 (Boolean Ring Alternative).

IV-E Two-Level Hashing for Scalability

Definition 27 (Two-Level Hash Structure).

Theorem 28 (Two-Level FPR).

IV-F Unified Hash Construction

Definition 29 (Hash-Based Bernoulli Type).

IV-G Privacy-Space Trade-off

Theorem 30 (Uniformity from Inverse-Frequency).

Remark 31 (Theoretical Foundation).

IV-H Cardinality Estimation

V Implementation

VI Evaluation

VI-A Experimental Setup

VI-B Performance Benchmarks

VI-C Scalability Analysis

VI-D Security Evaluation

VI-E Limitations and Attack Vectors

Remark 32 (When HBOS is Appropriate).

VI-F Comparison with Alternatives

VII Applications

Boolean Algebra over Trapdoor Sets: A Practical Framework for
Privacy-Preserving Set Operations with Probabilistic Guarantees